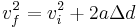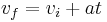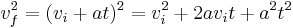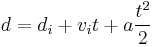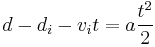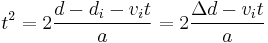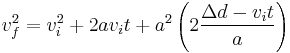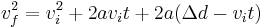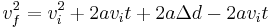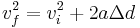Torricelli's equation

Not to be confused with Torricelli's law, Torricelli's theorem, Torricelli's trumpet, or Torricelli point.

Torricelli's equation is an equation created by Evangelista Torricelli to find the final velocity of an object moving with a constant acceleration without having a known time interval.

The equation itself is:

v_f^2 = v_i^2 %2B 2 a \Delta d \,

Derivation

Begin with the equation for velocity:

v_f = v_i %2B at\,\!

Square both sides to get:

v_f^2 = (v_i %2B at)^2 = v_i^2 %2B 2av_it %2B a^2t^2\,\!

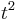The term t^2\,\! appears in the equation for displacement, and can be isolated:

d = d_i %2B v_it %2B a\frac{t^2}2
d - d_i - v_it = a\frac{t^2}2
t^2 = 2\frac{d-d_i - v_it}{a} = 2\frac{\Delta d - v_it}{a}

Substituting this back into our original equation yields:

v_f^2 = v_i^2 %2B 2av_it %2B a^2\left(2\frac{\Delta d - v_it}{a}\right)
v_f^2 = v_i^2 %2B 2av_it %2B 2a(\Delta d - v_it)
v_f^2 = v_i^2 %2B 2av_it %2B 2a\Delta d - 2av_it\,\!
v_f^2 = v_i^2 %2B 2a\Delta d\,\!

See also

External links